Když se podíváme na dluhopisy prodávané na pražské burze, uvidíme tam ceny jako 102 %, 98 % a tak dále. Jedná se o ceny dluhopisů, za které si je lze koupit, vyjádřené jako % jejich jmenovité hodnoty. Důvody, proč se tržní cena dluhopisu na sekundárním trhu odchyluje od jmenovité hodnoty (přestože vyplácený úrok je stále stejný) jsou v zásadě dva. Prvním jsou měnící se tržní podmínky, zejména prostředí úrokových sazeb.
Dluhopis je pouze jedna z investičních příležitostí, kam na nějakou dobu uložit své peníze, které neustále konkurují jiné alternativy na trhu, ale dluhopisy jako takové si konkurují i samy sobě navzájem. A to i ty, které vydává ta samá firma, jen v různých časech. A to i v případě, že je tato firma v čase stále stejně kreditně kvalitní. Vše je to o tom, jaká je aktuálně úroková míra v ekonomice.
Druhým hlavním důvodem je pak právě změna kreditního rizika té samé firmy. Pokud se její hospodářská situace a tím pádem i bonita v čase zhoršuje, mají dnes dluhopisy této firmy menší hodnotu, než když vyšly třeba před třemi lety, protože dnes by investoři požadovaly vyšší výnos ve formě vyšší rizikové přirážky. Dluhopisy ale nesou stále stejný kupón, a tak se musí tato změna projevit na ceně.
Odchýlení tržní ceny od jmenovité hodnoty dluhopisu může mít ale i další, druhotné důvody, a to i pokud předpokládáme v čase stejné úrokové prostředí i stejnou bonitu. Například nějaké „luxusní kousky“ se mohou na burze nabízet za vyšší než nominální cenu téměř okamžitě po úpisu, pokud byl o emisi opravdu velký zájem (jako jsme letos viděli na příkladu Českých drah nebo Accolade). Dalším důvodem je likvidita. Většina (zejména horších) bondů na trhu není nijak závratně likvidní a proto se prodávají spíše se slevou. Když má v případě některých dluhopisů problém prodat je i samotný emitent (a to i přestože mu často za pěkné peníze pomáhá finanční distribuce), jak má pak takový bond střelit někdo, kdo si ho koupil za 10 tisíc korun? Navíc pokud se ani neprodává na burze a investor si musí kupce hledat svépomocí. Jak se ale k takové tržní ceně vlastně dochází?
Příklad s poklesem úrokových sazeb:
Dluhopis má na rozdíl od akcie jasně stanovené fixní výnosy, z pohledu oceňování na sekundárním trhu je ale mnohem víc neintuitivní. Představte si, že v roce 2024 držíte šestiletý dluhopis ve jmenovité hodnotě 10 tisíc korun úročený sazbou 12 % p.a., který vyšel v roce 2023 a má tedy ještě pět let do splatnosti. Nyní si představte, že tento dluhopis vyšel v době vyšších úrokových sazeb, než jsou ty současné. Ta samá firma nyní za nové a stejně kvalitně připravené pětileté dluhopisy nabízí 10 %, což je oproti minulému roku, kdy emitovala ty samé bondy za 12 % ročně, docela propad. Předpokládejme, že pokles nabízeného výnosu je dán změnou úrokových sazeb v ekonomice, a nikoliv zlepšením její bonity, která je stejná jako před rokem. Ten samý bond se stejnou dobou do splatnosti úročený sazbou 12 % se díky tomu stal na trhu mnohem atraktivnějším.
Máme tedy dluhopis úročený 12 % ročně a nové bondy stejné kvality se stejnou dobou do splatnosti se nabízí za 10 % ročně. Těchto 10 % je naše IRR (internal rate of return), nebo u dluhopisů také YTM (yield to maturity). V podstatě jde o minimální zhodnocení dané investice, které jsou investoři ochotni akceptovat. Je to minimální výnos, který jste u dané investiční příležitosti ochotni přijmout po zhodnocení všech alternativ.
Jak tedy kalkulovat tržní cenu? Pro zjednodušení předpokládáme roční frekvenci výplaty bondů, i když v praxi jsou často úročeny pololetně i čtvrtletně. Pro výpočet tržní ceny dluhopisu musíme nejdřív identifikovat budoucí peněžní toky. U této obligace dostáváme každoročně úrokovou platbu 1200 korun a na konci dostanete zpět jmenovitou hodnotu 10 tisíc korun:
| Rok | 2024 | 2025 | 2026 | 2027 | 2028 |
| Cash flow | 1200 Kč | 1200 Kč | 1200 Kč | 1200 Kč | 11 200 Kč |
Tyto cash inflow toky musíme diskontovat očekávanou výnosovou mírou (v tomto případě oněch 10 %, tedy IRR) k jejich současné hodnotě. Rovnice vypadá následovně, přičemž r je naše IRR.
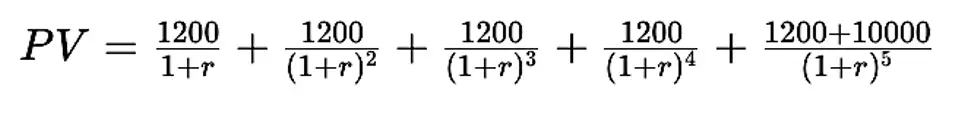
Po dosazení IRR ve výši 10 % vypadá rovnice následovně:
Po kalkulaci dostaneme číslo 10 758 korun, což je naše současná hodnota. V podstatě to říká, kolik by někdo za dluhopis musel zaplatit, aby se mu zhodnotil 10 % ročně až do splatnosti. Nominálně sice nese úrok 12 %, ale po zaplacení vyšší ceny technicky oněch 10 % ročně. Cena je tedy 107,58 % nominálu. Počítat rovnice ale nemusíte, na spočítání tržní ceny bondu už dnes existují online kalkulačky.
Příklad s růstem úrokových sazeb:
Dejme si jiný příklad, kde bude tržní cena bondu naopak nižší než nominál. Pokud koupíme pětiletý bond v době emise na primárním trhu za 100 % nominální ceny a nese fixní roční výnos třeba 5 %, je IRR rovna fixní úrokové sazbě. Po nějaké době se však můžeme dostat do jiného úrokového prostředí. Pokud to otočíme a budeme nyní předpokládat, že sazby porostou, tak se nově emitované dluhopisy stejné kreditní kvality a stejné doby do splatnosti budou ve vyšším úrokovém prostředí nabízet za atraktivnější výnos, např. 6 % ročně.
Náš bond ale nese 5 % a na tom se nic nezmění. Aby tedy těmto novým a stejně kvalitním bondům emitovaným za lepší úrok mohl konkurovat, musí se prodat za nižší cenu, než je 100 % nominálu. Jenom tato sleva dokáže vyrovnat rozdíl v kuponových platbách, které nám chodí při sazbě 5 % versus při 6 procentech. Máme tedy dluhopis nesoucí roční výnos 5 % s např. třemi zbývajícími lety do splatnosti, ale my chceme, aby nesl alespoň 6 %. Tedy aby měl IRR alespoň 6 %. Jak jsme si řekli, fixní výnos ve výši 5 % změnit nemůžeme.
Když ale dluhopis prodáme za 97,32 % nominálu (a na konci dostaneme 100 % nominálu), ony 2,68 procentní body rozdílu v ceně kompenzují právě nižší nabízený fixní roční výnos oproti tomu, co nabízí současná konkurence. Bond má tedy jmenovitou hodnotu např. 10 tisíc korun a prodá se za 9 732 korun. Tím nese držiteli 6 % ročně, i když je nominální úrok jen 5 %.
Jak do toho vstupuje naběhlý úrok?
Až doposud jsme předpokládali, že dluhopisy se obchodují v den výplaty kupónu. V praxi se však dluhopisy většinou obchodují mimo tyto dny. Předpokládejme, že dluhopis z druhého příkladu prodáváme o půl roku později, než v původním příkladu. Tedy že mu zbývá pouze 2,5 let do splatnosti. Pokud si ho koupíme za původní cenu, dostaneme za půl roku roční výnos za celý uplynulý rok. Jenomže my bychom tento dluhopis drželi jen půl roku, první polovinu jej držel původní majitel. Tedy si odčekal polovinu tohoto výnosu. Zde vstupuje do hry něco, čemu se říká alikvotní úrokový výnos (AÚV).
Pro zjednodušení předpokládejme, že rok má 365 dnů. V původním příkladu jsme bond koupili 1.1.2024 a je splatný 1.1.2027. Tedy přesně za tři roky. V době prodeje (1.1.2024) dostal prodávající svou poslední výplatu kupónu za celý předešlý rok a poté jsme dostali do ruky dluhopis my a na další výnos čekáme celý další rok. Kupóny jsou vyřešené, řeší se jen cena.
Praxe ale bývá složitější. Dejme tomu, že dluhopis koupíme ne 1.1.2024, ale 1.7.2024, tedy o půl roku později. Frekvence výplaty je ale pro zjednodušení jen jednou ročně, vždy k 1.1. daného roku. Pokud by nám prodávající tento dluhopis prodal 1.7.2024, my bychom za půl roku (tedy k 1.1.2025) „shrábli“ výnos za celý uplynulý rok. Dluhopis bychom ale drželi jen půl roku, tu první polovinu roku si odčekal prodávající. Kupónová výplata k 1.1.2025 za celé výnosové období (uplynulý rok) činí v našem případě 10 000 Kč x 5 % = 500 korun. Vzhledem k tomu, že kupón roste s každým dalším takto „odčekaným“ dnem (takzvaně nabíhá), a rok předpokládáme jako 365 dní, naběhne nám každý den výnos cca 1,37 korun (=500/365), což je po prvních šesti měsících přesně 250 korun. Na ty nemáme nárok, protože jsme tento dluhopis v období od 1.1.2024 do 30.6.2024 nedrželi my, ale prodávající.
Naše tržní cena činí v tomto novém příkladu 9770 korun bez naběhlého úroku. Tržní cena se zde trochu mění od původní hodnoty, protože bond kupujeme o půl roku později. To samozřejmě změní i výpočet čisté současné hodnoty, jejíž původní vzorec vypadal takto:
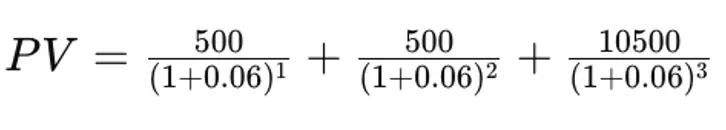
a s půlročním odkladem nákupu takto, jelikož se mění časová hodnota cash inflow toků:
Na dluhopisovém trhu se používají pojmy „clean price“ a „dirty price“, aby se rozlišily způsoby, jakými je cena dluhopisu uváděna mimo datum výplaty kupónu. 9770 korun je „clean price“, tedy cena bez naběhlého úroku. Kromě této ceny má ale prodávající nárok i na svou část naběhlého výnosu, tedy na svých 250 korun. Celková cena (dirty price) činí 10 020 korun.
Redakční články jsou ty, který vznikají jako unikátní obsah pro naše čtenáře a jsou vytvářeny zcela a pouze naší redakcí. Veškerá finanční data a informace byly získány z veřejných zdrojů jako je server Justice.cz, ČNB, webové stránky, účetní podklady a výroční zprávy jednotlivých společností.
